CSC270 Root Finding

Mean Value Theorem (MVT)

Theorem

  If f() is continuous and differentiable on an interval [a,b], then
  there exists some c in (a,b) such that

                 f(b) - f(a)
         f'(c) = -----------
                    b - a

  Equivalently,

         f(b) - f(a) = f'(c) (b - a)


Above, (f(b)-f(a))/(b-a) is just the slope between point (a,f(a)) and
point (b,f(b)).  This is the average, or `mean', slope of the function
between those two points.  The theorem simply says that there is a
point in (a,b) for which the function *has* that mean slope.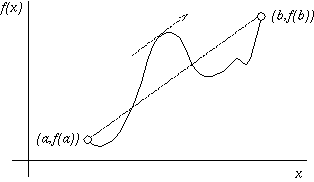





Taylor series

Suppose we want to model a function f() near a point c.  Suppose
further that f() is infinitely differentiable at c and that we know
f'(c), f''(c), and so on.

Then we can use a polynomial function p() with the same value and
derivatives to *approximate* f().  For this polynomial, we have the
following constraints:

  p(c) = f(c)
  p'(c) = f'(c)
  p''(c) = f''(c)
  and so on.

A polynomial that satisfies these constraints is the ``Taylor
Polynomial of degree n'':

                                              2            (n)        n
                                  f''(c) (x-c)            f  (c) (x-c)
  p_n (x) = f(c) + f'(c) (x-c) +  ------------- + ..... + -------------
                                        2!                      n!

If n goes to infinity, we get the Taylor Series.  For many functions
(among them the polynomials), the Taylor Series converges to the
function.  That is, p_n(x) = f(x) for all x.  In this course, we won't
characterize the functions for which the Taylor Series converges.

When approximating a function f() with the Taylor polynomial p_n() of
degree n, the *residual* is

  r_n(x) = p(x) - f(x)

Taylor's Theorem says that if the n derivatives of f() exist in an
interval [a,b] that contains c, then there is *some* x_{max} in [a,b]
such that

               (n+1)            n+1
            | f   (c) (x_{max}-c)  |          n+1
  r_n(x) <=   ------------------      * | (x-c)  |
                     (n+1)!

for all x in [a,b].  This means that the residual is bounded by some
constant (a function of x_{max}) times (x-c)^{n+1}.  In other words,
the residual is ``of the order of (x-c)^{n+1}, written:

                n+1
  r_n is O( (x-c)  )

This gives us an idea of how fast the residual diminishes as x 
approaches c.



Newton's method of root finding
  

[Readings section 2, pages 412-421]

Suppose an algorithm computes successive approximations, x1, x2, x3,
..., to a root of a function f().  Consider the first-order Taylor
expansion about the i^th appoximation:

  p(x) = f(x_i) + f'(x_i) (x - x_i)

Since p(x) is approximately f(x), we set p(x) to zero and solve for
the root x:

            f(x_i)
  x = x_i - -------
            f'(x_i)

Since p() is only an approximation to f(), this root x is only an
approximation to the root of f().  So we'll use it as our next
approximation, x_{n+1}.  If p() is a ``good'' approximation of f(),
x_{n+1} should be a better approximation to f()'s root than was x_n.

This is called Newton iteration.  The algorithm computes

  x_1 = x_0 - f(x_0) / f'(x_0)
  x_2 = x_1 - f(x_1) / f'(x_1)
  x_3 = x_2 - f(x_2) / f'(x_2)
  and so on.

Intuitively, x_{n+1} is chosen as the point where the tangent at
(x_n,f(x_n)) cuts the x axis.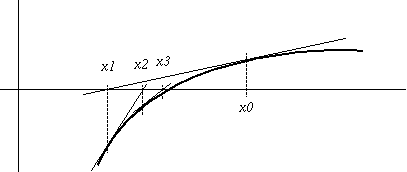



Theorem [page 64]

  If x_n is in an interval [a,b] such that

    - f(a) f(b) < 0
    - f' is not zero in [a,b]
    - f'' doesn't change sign in [a,b]
    - f(a)/f'(a) < b-a and f(b)/f'(b) < b-a

  then the Newton iteration converges to a root of f().

Newton iteration converges quadratically, provided the initial guess
x_0 is ``good enough''.  To show this requires a bit of calculus.  In
brief, if the error in the n^{th} iteration is e_n, then

                                2
  e_{n+1} is proportional to e_n



Secant method of root finding

The Newton method requires the first derivative f'(), which is
sometimes not available to a program.  The secant method avoids this
problem.

To get x_{n+1} from x_n, the Newton method followed the tangent at x_n
until it intersected the x axis.  The secant method will approximate
the tangent by drawing a line between two close points on the curve
f(x).  Such a line is a `secant'.  Note that, as the two points get
closer, the secant approaches the tangen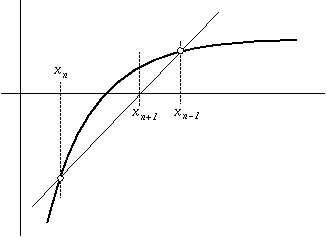t.



Thus f'(x_n) is approximated by


              f(x_n) - f(x_{n-1})
  f'(x_n)  ~  -------------------
                 x_n - x_{n-1}

and the Newton iteration is modified as follows:


  x_{n+1} = x_n - f(x_n) / f'(x_n)

                              x_n - x_{n-1}
          ~ x_n - f(x_n) * -------------------
                           f(x_n) - f(x_{n-1})

            x_{n-1} f(x_n) - x_n f(x_{n-1})
          = -------------------------------
                  f(x_n) - f(x_{n-1})

As with Newton iteration, the secant method uses for its next
approximation to the root the intersection of the secant with
the x axis.

The secant method converges a bit slower than the Newton method:

                                1.62
  e_{n+1} is proportional to e_n

As with the Newton method, there are situations in which the
secant method will not converge to the root.