[TEXT: 208-210, 217-222]
Rotation about an arbitrary point
Find the transformation that rotates by an angle theta about
a point P(x,y):
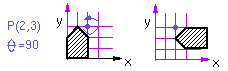
Let's choose to describe all transformations w.r.t. a fixed set of axes:
- translate P to origin: trans(-2,-3,0)
- perform rotation: rot(z,90)
- translate P back: trans(2,3,0)
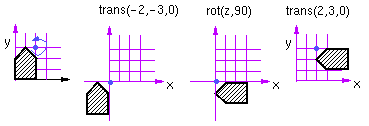
T = trans(2,3,0) rot(z,90) trans(-2,-3,0)
Rotation about an arbitrary axis
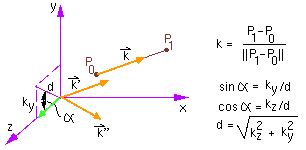
- translate axis k to origin: trans(-P0)
- rotate about x-axis to bring axis k' to lie in xz plane:
rot(x,alpha)
The amount of rotation is determined by looking at the projection
on the yz plane. Alpha need not actually be calculated; it's
sine and cosine can be evaluated directly.
- rotate about y-axis to align axis k'' with z-axis:
rot(y,-beta).
As in the previous step, we need not actually calculate beta.

- perform the desired rotation: rot(z,theta)
- reverse all the other steps
Overall Transform
trans(P0) rot(x,-alpha) rot(y,beta) rot(z,theta) rot(y,-beta) rot(x,alpha) trans(-P0)




