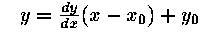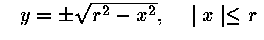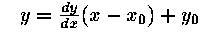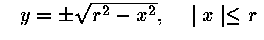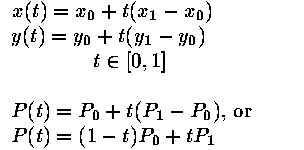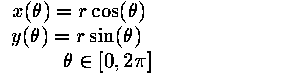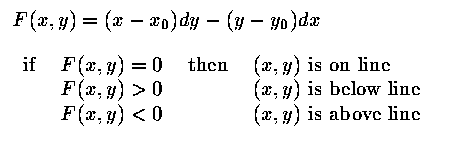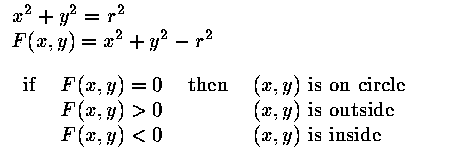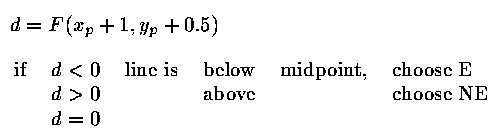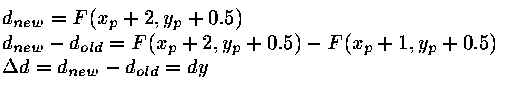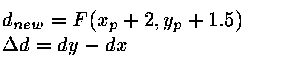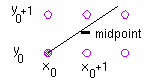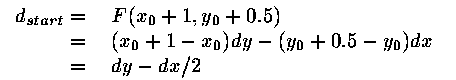Representations for Lines and Curves
A prelimenary step to drawing lines and curves is choosing a suitable representation
for them. There are three possible choices which are potentially useful.
Explicit: y = f(x)
| line |
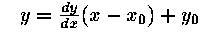 |
| circle |
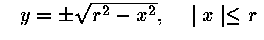 |
Parametric: x = f(t), y = f(t)
| line |
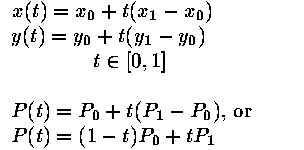 |
| circle |
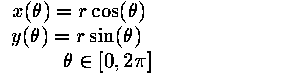 |
Implicit: f(x,y) = 0
| line |
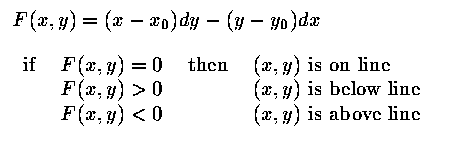 |
| circle |
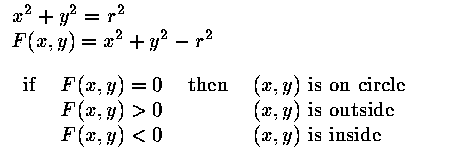 |
Optimal Line Drawing
Drawing lines on a raster grid implicitly involves approximation. The general
process is called rasterization or scan-conversion. What
is the best way to draw a line from the pixel (x1,y1) to (x2,y2)? Such
a line should ideally have the following properties.
-
straight
-
pass through endpoints
-
smooth
-
independent of endpoint order
-
uniform brightness
-
brightness independent of slope
-
efficient
A Straightforward Implementation
DrawLine(x1,y1,x2,y2)
int x1,y1,x2,y2;
{
float y;
int x;
for (x=x1; x<=x2; x++) {
y = y1 + (x-x1)*(y2-y1)/(x2-x1)
SetPixel(x, Round(y) );
}
}
A Better Implementation
DrawLine(x1,y1,x2,y2)
int x1,y1,x2,y2;
{
float m,y;
int dx,dy,x;
dx = x2 - x1;
dy = y2 - y1;
m = dy/dx;
y = y1 + 0.5;
for (x=x1; x<=x2; x++) {
SetPixel(x, Floor(y) );
y = y + m;
}
}
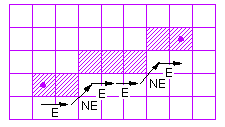
The Midpoint Algorithm
The midpoint algorithm is even better than the above algorithm in that
it uses only integer calculations. It treats line drawing as a sequence
of decisions. For each pixel that is drawn, the next pixel will be either
E or NE, as shown below.
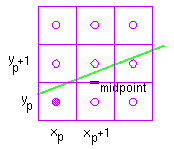
The midpoint algorithm makes use of the the implicit definition of the
line, F(x,y) = 0. The E/NE decisions are made as follows.
 define
define
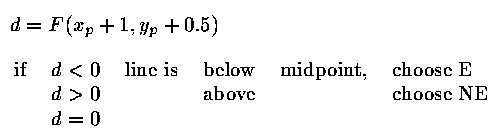
if E is chosen,
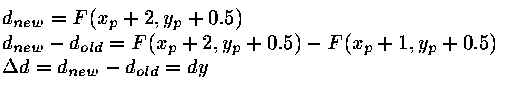
if NE is chosen,
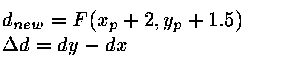
The process repeats, stepping along x, making decisions whether to
set E or NE pixel.
Initialization
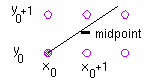
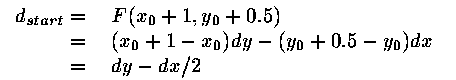
Now we would like an integer-only algorithm.
Define

Midpoint Algorithm
The following algorithm produces the desired results for lines having x1
less than x2 and a slope less or equal to 1.
drawline(x1, y1, x2, y2, colour)
int x1, y1, x2, y2, colour;
{
int dx, dy, d, incE, incNE, x, y;
dx = x2 - x1;
dy = y2 - y1;
d = 2*dy - dx;
incE = 2*dy;
incNE = 2*(dy - dx);
y = y1;
for (x=x1; x<=x2; x++) {
setpixel(x, y, colour);
if (d>0) {
d = d + incNE;
y = y + 1;
} else {
d = d + incE;
}
}
}