We will determine ![]() for any concave down function
for any concave down function ![]() .
Since g is concave down,
.
Since g is concave down, ![]() .
Let
.
Let ![]() ;
we assume that
;
we assume that ![]() , so
we may take
, so
we may take ![]() .
A simple proof by contradiction, which follows, shows that
.
A simple proof by contradiction, which follows, shows that
![]() is an upper bound for g,
excepting
is an upper bound for g,
excepting ![]() :
:
![]()
Assume that there is a point ![]() such that
such that ![]() .
Let
.
Let ![]() , so
, so ![]() .
Furthermore,
.
Furthermore, ![]() and
and ![]() imply that
imply that ![]() .
.
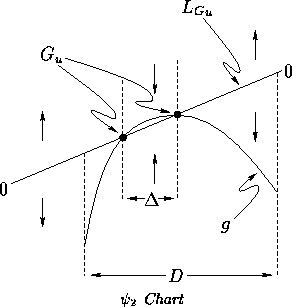
The assumptions made do not overly restrict the applicability of the proof.
For differentiable g and constant ![]() ,
the bound is optimal when
,
the bound is optimal when ![]() ;
for other reasonable choices of
;
for other reasonable choices of ![]() , the optimal bound
is similarly easy to determine. See section
, the optimal bound
is similarly easy to determine. See section ![]() for details.
for details.
| Jeff Tupper | March 1996 |