4.3.3 Linear Interval Arithmetic

A similar algorithm may be enacted, but with linear interval arithmetic used to evaluate . The algorithm proceeds as before, unless

in which case the relationship between and the system parameters x and y may allow for some pixels to be set to either or . An example follows:

The dotted lines indicate the constraints determined by the linear interval evaluation of S. Pixels which lie outside of these constraints are set to . A pixel may be set to if the evaluation of has shown that S is continuous over and that attains both signs. This is seen visually when the constraints divide the pixel into three regions; the constraint region includes no corners. Such determination mimics the one-dimensional case, described in section .

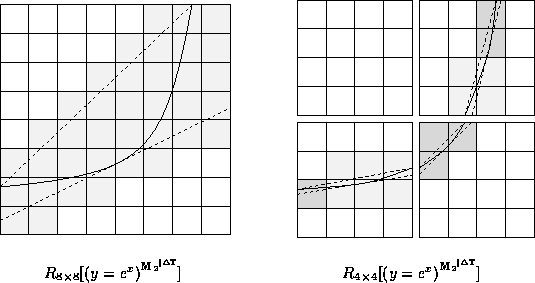
Pixel assignment may be rapidly performed by using provided graphics primitives. When

the appropriate rectangle is rendered; when

appropriate polygons are rendered. As demonstrated earlier, continuity information may also allow some pixels within the constraint region to be set when rendering equations. Usually, a white polygon on either side of the constraint region is rendered. With intimate knowledge of the provided graphics primitives, such rendering may be straightforward.

Slight perturbation of the polygon may ensure that pixels are not set incorrectly, as the following diagram suggests:

The affected pixels are shown in dark grey; unaffected pixels are not shown.

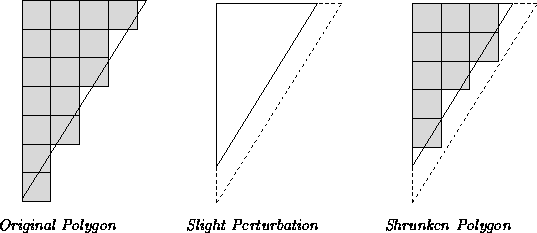
Precise, rapid pixel control is posssible; a rapid polygon rendering may be followed by manipulation of the pixels along the perimeter of the polygon. A precise rendering of the graph may be deferred until the clusters describe small collections of pixels; polygon perturbation may ensure all intervening renderings still represent G.

Employing sophisticated interval arithmetics requires sophisticated graphics primitives; requires primitives which render conic sections. Unavailable graphics primitives may be implemented, but such implementation negates part of the advantage of using a more sophisticated interval arithmetic. When using sophisticated interval arithmetics, demotions may be used to reduce the variety of graphics primitives needed: allows to be used with polygon-filling primitives; and allow and to be used with rectangle-filling primitives.

Jeff Tupper

March 1996