Traditional approaches to rendering functions
sample the given function g at various
places, by computing ![]() .
After sampling, a rendering is produced by
appropriately connecting the samples.
We deam such approaches unsatisfactory,
as the produced graph may mislead the viewer
as to the nature of G.
Some examples follow:
.
After sampling, a rendering is produced by
appropriately connecting the samples.
We deam such approaches unsatisfactory,
as the produced graph may mislead the viewer
as to the nature of G.
Some examples follow:
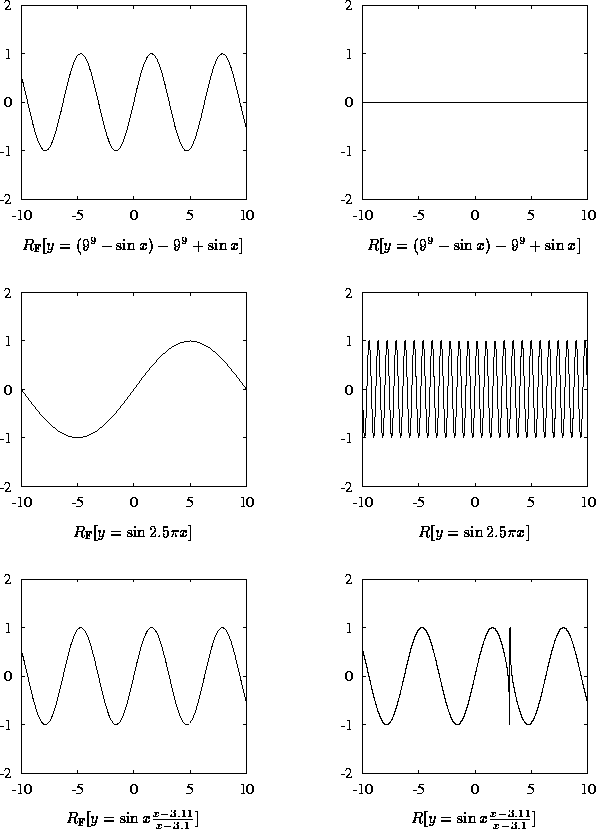
These approaches typically break down when investigating minute details of the graph, as the following renderings illustrate:
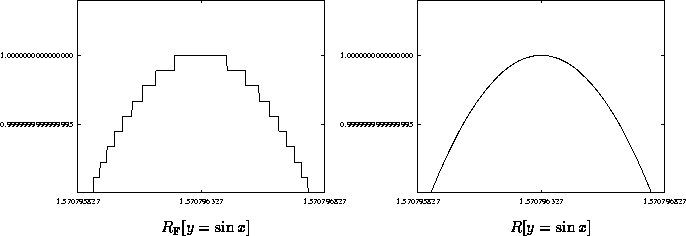
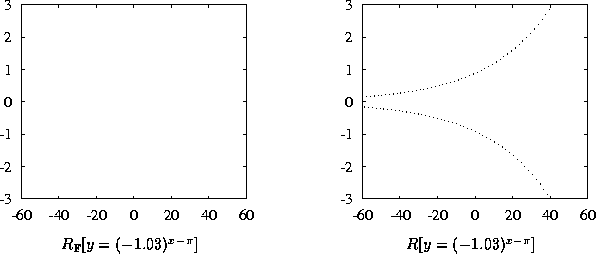
The renderings produced for the above examples finish with each pixel determined exactly, excepting that which displays fine-scale detail. With that function, a course approximation is generated, which contains the true curve. An erstwhile interval-based renderer may increase the precision of the underlying number system, as needed.
More sophisticated sampling algorithms may be similarly fooled, although with more convoluted examples. Without assumptions as to the shape of G, a finite number of floating-point samples gives no information, other than the samples actually computed. Samples computed using floating point rarely lie within G.
| Jeff Tupper | March 1996 |