




Next: 2.9.2 Three Valued Logic
Up: 2.9 Generalized Interval Arithmetic
Previous: 2.9 Generalized Interval Arithmetic
The symbol 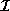 is a transformational
operator which transforms number systems into interval
number systems. Floating point
interval arithmetic,
is a transformational
operator which transforms number systems into interval
number systems. Floating point
interval arithmetic,  , can be rewritten
as
, can be rewritten
as  ; while real interval arithmetic,
; while real interval arithmetic,
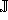 , can be rewritten as
, can be rewritten as  .
As
.
As  denotes a number system,
denotes a number system,  denotes an interval number system.
denotes an interval number system.
Interval arithmetic has been generalized through
this simplification.
Consider the number system
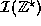 which denotes an interval system where
the endpoints are extended integers:
which denotes an interval system where
the endpoints are extended integers:
Infinities are useful in the underlying number system since
intervals may need to describe arbitrarily distant numbers.
Without them, some interval operators are forced to
be only partially defined.
Consider the interval number system 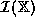 ;
the previous example had
;
the previous example had 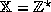 .
The interval inclusion property for n-ary
function g is clearly stated as:
.
The interval inclusion property for n-ary
function g is clearly stated as:
The argument  is considered to vary over the
domain of g.
This property is equivalent to the inclusion
property for both real and floating point intervals.
is considered to vary over the
domain of g.
This property is equivalent to the inclusion
property for both real and floating point intervals.
The interval extension of an n-ary function
g is defined as:
The demotions  and
and  are
used since the derived interval endpoints will need to
be ``rounded out'' to ensure the endpoints
are valid and of the correct type. The argument
are
used since the derived interval endpoints will need to
be ``rounded out'' to ensure the endpoints
are valid and of the correct type. The argument
 is considered to vary over the domain of g.
Demotions are not needed if the underlying
number system is no poorer than the number system
which the result of g belongs to, as was seen
when g was a real valued function and the interval
system was
is considered to vary over the domain of g.
Demotions are not needed if the underlying
number system is no poorer than the number system
which the result of g belongs to, as was seen
when g was a real valued function and the interval
system was 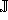 .
.





Next: 2.9.2 Three Valued Logic
Up: 2.9 Generalized Interval Arithmetic
Previous: 2.9 Generalized Interval Arithmetic
![]() is a transformational
operator which transforms number systems into interval
number systems. Floating point
interval arithmetic,
is a transformational
operator which transforms number systems into interval
number systems. Floating point
interval arithmetic, ![]() , can be rewritten
as
, can be rewritten
as ![]() ; while real interval arithmetic,
; while real interval arithmetic,
![]() , can be rewritten as
, can be rewritten as ![]() .
As
.
As ![]() denotes a number system,
denotes a number system, ![]() denotes an interval number system.
denotes an interval number system.
![]() which denotes an interval system where
the endpoints are extended integers:
which denotes an interval system where
the endpoints are extended integers:
![]()
![]() ;
the previous example had
;
the previous example had ![]() .
The interval inclusion property for n-ary
function g is clearly stated as:
.
The interval inclusion property for n-ary
function g is clearly stated as:
![]()
![]()