2.9.3 Linear Intervals

The transformational operator will be extended to further generalize interval arithmetic.

We envision numbers as a tool used to describe things. Many of the things described by numbers are parameterized. For example, we may be using a number to describe the mass of an iron ball. The iron ball can be parameterized by its radius. We will bring these parameters into our number system. This integration of parameters into numbers will give us hints as to how numbers depend on the parameters. These hints will enable the new interval routines to return much tighter results.

To start, we will consider a number system with a single parameter   . The parameter can vary from zero to one, and is a real number. Again, as a starting point we will consider only linear relationships between the parameter and the value's bounds. This new number system, using real numbers as the underlying number system, is denoted by or . The subscript, , states that a linear relationship is used; the greek letter signifies the parameter of the linear function, while the latin letters p and q signify coefficients of the linear function.

A linear interval is described by a lower and upper endpoint, each of which is a linear function of . The coefficients of the linear functions must be numbers of the underlying system .

The semantics of the interval   is: when parameter has value k, the interval represents a fixed real number between a+bk and c+dk. This can be stated formally as:

for real number x. Although the upper and lower endpoints of interval are linear functions of , the real number represented by the interval may not be a linear function of the parameter . The intervals cannot collapse. The interval between the lower and upper bound must be well-defined:

This follows from the original statement that intervals must have non-negative width:

The upper and lower functions must both be well-defined over [0,1]:

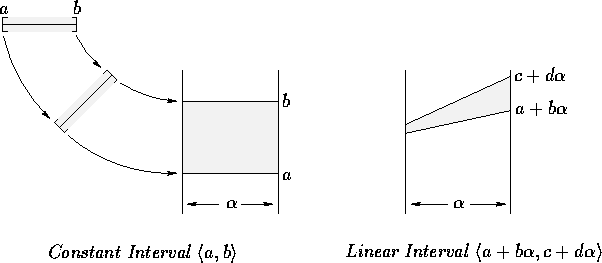
A picture may soothe the intuition. Associate the interval with the closed set [a,b], of extended real numbers. The free variable may be accommodated by introducing a new dimension. The interval does not interact with this new dimension, although the interval does. The earlier intervals may now be regarded as ``constant intervals''.

An example is appropriate. Consider the problem of determining the range of an arbitrary function over the domain [0,1]. The parameter in this case is the argument to the function. The range may be computed by simply evaluating the function with x being a number representing the domain of interest, [0,1].

Since varies over [0,1], the linear function represents the domain completely: every element of the domain [0,1] is represented by , for some value of . It follows that the linear interval represents the domain: every element of the domain is contained in the interval . The constant interval represents the domain since every element of the domain is represented by an element of .

Consider the simple function g(x) = x - x. So, with , this proceeds as follows:

The resulting bound for the range is [0,0], which is the actual range. Using this would proceed as follows:

The resulting bound for the range is [-1,1], which is valid, but definitely not optimal. To determine the range of g over the domain [a,b], the domain would be represented by the linear interval , or the constant interval . The domain may also be represented by the linear interval . Any valid linear interval representative of the domain [a,b] must contain either or ; unless it also represents a larger domain D, .

The linear real interval number system may be denoted by   . The notation follows from the denotation   for the linear floating point interval number system:

A linear interval model of an n-ary function satistfies the inclusion property if  

Since is a function of , is well defined as a closed real interval:

The linear interval extension of the n-ary function g is defined as follows:

The lower and upper bounds l and u are functions of . The lower bound bounds from below; the range of is , and is therefore a function of . Although l is a function of it is not guaranteed to be linear, or even continuous. The demotion from an arbitrary function to a linear function is significant. The demoted bounds from below while the demoted bounds from above. In both cases, varies from zero to one.  

The demotions and are significant in the definition of interval extension because there is no best demotion available. This is drastically different from the demotions and used in the definition of floating point interval extensions. When demoting an extended real to a float, there is a particular floating point number which is the best choice. When rounding down, the largest floating point number less than or equal to the extended real is chosen. The best choice when demoting an arbitrary extended real function l to a linear extended real function depends on how will be used. This significantly changes the character of the interval extension. It can no longer be used to show an interval model is optimal in general, although it may be used to show that an interval method is suboptimal.

Jeff Tupper

March 1996