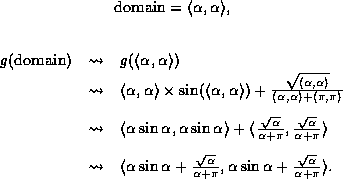Next: 2.10 Generalized Floating Point Interval
Up: 2.9 Generalized Interval Arithmetic
Previous: 2.9.7 Functional Intervals
The most general choice of f is to allow arbitrarily
complex functions. Another way to view this is to
have f as a universal function with an infinite
number of coefficients:
Of course, at any point in a computation only a finite
number of coefficients are non-zero. A method
of this form could completely avoid any difficult
decisions by just ``pushing'' the computation into
the interval symbolically, as shown in the example following.
Consider using such a system with our simple
algorithm for determing a function's range over
a given domain. An example problem instance
is to determine the range of  ,
,
over the domain [0,1].
The algorithm would proceed as follows:
Although the algorithm returned a description of the tightest
bounds possible on the range of g, the results are
obviously not of much use. We are no further along than
when we started.
Symbolic computation is not a panacea. Although
the operator models and demotion operators would
be trivial to implement, interpreting the results
becomes difficult. Symbolic simplification could
be performed by the interval operators.





Next: 2.10 Generalized Floating Point Interval
Up: 2.9 Generalized Interval Arithmetic
Previous: 2.9.7 Functional Intervals
![]()
![]()
![]() ,
,
![]()