2.13.1 Interval Inclusion and Extension

Next: 2.13.2 Bumpy Functions Up: 2.13 Interval Sets Previous: 2.13 Interval Sets

2.13.1 Interval Inclusion and Extension

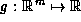A model satisfies the inclusion property for function if

Note that for

to be contained in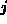

,

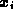may be in any member of

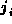. This follows from the definition of vector containment.

The interval extension of g can be defined as before:

This definition hides a great deal in the seemingly innocuous demotions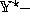

and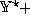

. Consider the case

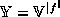. Perfect demotion operators

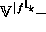and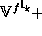

can be defined, as follows:

The perfect demotion operators describe a demoted function as an infinite collection of points (denoted above as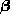

). Although the associated perfect demotion operators

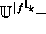and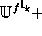

would describe a function by a finite number of intervals, the size of the descriptions would be unmanageable.

Partial functions may be handled in a natural manner, as the following examples show, for :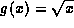

A good model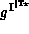

of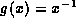

would behave as follows:

A poor model would behave as follows:

Interval sets may be viewed as a simplification, or a generalization, of extended interval arithmetic, as defined in [32].

Next: 2.13.2 Bumpy Functions Up: 2.13 Interval Sets Previous: 2.13 Interval Sets

Jeff Tupper

March 1996