




Next: 3.2.17 Examples with a Partial
Up: 3.2 Constant Interval Arithmetic
Previous: 3.2.15 Periodic Functions
We have considered implementing a model 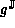 , given
, given  .
We now consider implementing
.
We now consider implementing  .
The property
.
The property 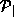 is of interest; let
is of interest; let 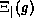 denote the domain of g, defined in terms of
denote the domain of g, defined in terms of 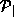 :
:
The function 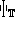 ,
when given
an interval j and a set
,
when given
an interval j and a set 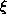 of extended real numbers,
produces a valid description of the relationship
between j and
of extended real numbers,
produces a valid description of the relationship
between j and 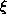 :
The relationship between j and
:
The relationship between j and 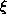 is that of containment,
formally defined as follows:
is that of containment,
formally defined as follows:
For the function 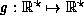 , an evaluation
of the model
, an evaluation
of the model  proceeds as follows:
proceeds as follows:
The resulting domain description d', 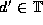 ,
is determined using d,
,
is determined using d, 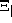 , and
, and 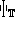 :
The resulting value v',
:
The resulting value v', 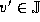 , depends on d'.
If
, depends on d'.
If 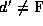 ,
the resulting value is given by the methods outlined earlier:
If
,
the resulting value is given by the methods outlined earlier:
If 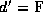 , the resulting value is arbitrary:
as
, the resulting value is arbitrary:
as 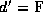 implies that
implies that  for all
for all
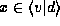 .
.





Next: 3.2.17 Examples with a Partial
Up: 3.2 Constant Interval Arithmetic
Previous: 3.2.15 Periodic Functions
![]() , given
, given ![]() .
We now consider implementing
.
We now consider implementing ![]() .
The property
.
The property ![]() is of interest; let
is of interest; let ![]() denote the domain of g, defined in terms of
denote the domain of g, defined in terms of ![]() :
:
![]()
![]()
![]()
![]()
![]() , an evaluation
of the model
, an evaluation
of the model ![]() proceeds as follows:
proceeds as follows:
![]()
![]()
![]()
![]()