A light source has the following spectral distribution:

in other words,
| P(L)=0.5, | 400nm < L < 500nm |
| P(L)=1.0, | 500nm < L < 600nm |
| P(L)=0.5, | 600nm < L < 700nm |
| P(L)=0, | elsewhere |
- [4 marks] Compute X,Y,Z, the CIE colour components.
The functions x(L), y(L) and z(L) are available online in tabular
form at:
http://www.dgp.toronto.edu/~ah/csc418/fall_1999/coursework/ciexyz.dat
Each line contains a wavelength L, and three values for x(L), y(L) and z(L). Use the code in
http://www.dgp.toronto.edu/~ah/csc418/fall_1999/coursework/a2q1.c
to read the data. - [1 mark] Compute x,y,z, the chromaticity coordinates for the source.
- [2 marks] Plot the colour on the CIE diagram (available online). Assuming white has (x,y)=(1/3,1/3), what is its dominant wavelength?
- [2 marks] Assuming the phosphors in a monitor have the following chromaticity
coordinates:
x y R 0.64 0.33 G 0.30 0.60 B 0.15 0.06 - [1 mark] What are the Y,I,Q components?
Consider the point P and the three coordinate frames O, A, and B below:
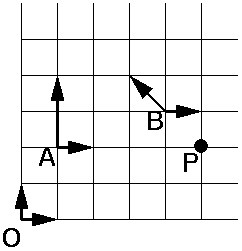
Notation: MRS is a 3x3 homogeneous matrix, and PR=(x,y,1) is a homogeneous point in coordinate frame S, such that
- [2 marks] Find the coordinates of P in the three frames.
- [3 marks] Find MOA, MOB, MAB and MBA.
- [2 marks] Succintly express MAB in terms of MOA and MOB.
Succintly express MAB in terms of MBA.
- each vertex must be transformed to viewing coordinates, projected, and then transformed to the viewport.
- geometric transformations dominate the cost, and scan conversion is handled by hardware.
- lighting and clipping calculations are free.
- triangles are specified in strips (see GL_TRIANGLE_STRIP).
Given the following camera parameters:
- Peye = (1.5, 1.7, 2.0)
- Pref = (0.5, 0.5, 0.5)
- Vup = (0.0, 0.0, 1.0)
- [3 marks] Construct the viewing matrix Mworld-cam.
- [2 marks] Assume the following projection matrix,
[1 0 0 0] [0 1 0 0] [0 0 1 0] [0 0 -1 0]
and project onto the image plane the eight vertices of an axis-aligned unit cube, with corners at (0,0,0) and (1,1,1). - [2 marks] After projection, lines which were parallel will appear to converge to a "vanishing point". The cube has three sets of parallel edges. Determine the coordinates of the vanishing points, on the image plane.
[4 marks] Write an openGL program to draw a hierarchical object with
at least 5 degrees of freedom. Sample code is available at:
http://www.dgp.toronto.edu/~ah/csc418/fall_1999/coursework/a2q5
[Bonus 1 mark]: Add degrees of freedom for the camera orientation.
[6 marks] The parametric equation for a ray starting at P and in direction
V is:
(x,y,z) = P + t V, 0 < t < infinity
Assuming:
- All objects are in viewing (camera) coordinates.
- The image plane is on the front clipping plane, and is bounded by a rectangle with corners at (-1,-1,-1) and (1,1,-1).
- The clipped image plane is displayed on an n x n raster of pixels,
- determine P and V for a ray from the eye through pixel (x,y).
- given a polygon whose vertices are p0, p1, ... pm, determine the parameters A,B,C,D of the equation Ax+By+Cz+D=0 for the plane containing it.
- determine the intersection T between the ray in (a) and the plane in (b).
- determine if the intersection T is inside the polygon:
- project T and all pi to one of the 3 (xy, yz, or xz) coordinate planes (which one is best?).
- perform a 2D point-in-polygon test.
http://www.dgp.toronto.edu/~ah/csc418/fall_1999/coursework/a2q6/a2q6.c