- 3 marks:
Consider a cubic curve defined by the following geometric constraints:
- passes through P1 at t=0
- passes through P2 at t=2/3
- passes through P4 at t=1
- has tangent T2 at t=2/3
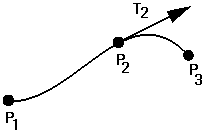
Write an expression for the basis matrix of the curve.
- 2 marks:
What is the convex-hull property of Bezier curves?
- 1 mark:
When rendering a Bezier curve, how can you use this property
to speed up clipping?
- 3 marks:
What is the geometric and parametric continuity of
these two curves:
C1(t) = [t3+t2+t, -t2+2t] C2(t) = [3t3+3t2+6t+3, t2-1]
Consider a graphics pipeline with the following view (world-to-camera) matrix and projection matrix:

Final image size: 512x512
Consider the line segment Pa Pb, with Pa=(1,1,-2) and Pb=(2,-1,-1) in WCS.
- 2 marks:
Write a set of parametric equations for the line segment,
in WCS.
- 2 marks:
Compute the endpoints of the line segment in VCS.
- 2 marks:
Compute the endpoints of the line segment in NDCS.
- 2 marks:
Calculate the midpoint of PaPb in VCS,
and transform this point to device coords.
- 2 marks:
Will this be the midpoint of the line on the device?
If yes, why? If not, which step in the graphics pipeline
makes a difference?
- 2 marks:
Suppose three coloured dots are printed on a sheet of paper,
one cyan, one magenta, and one yellow. If the paper is lit
with a blue light, what will be seen, qualitatively speaking?
- 3 marks:
Suppose a monitor has the following RGB-to-XYZ transformation
matrix:

- 2 marks:
Compute the monitor's colour gamut and sketch it on the CIE diagram.
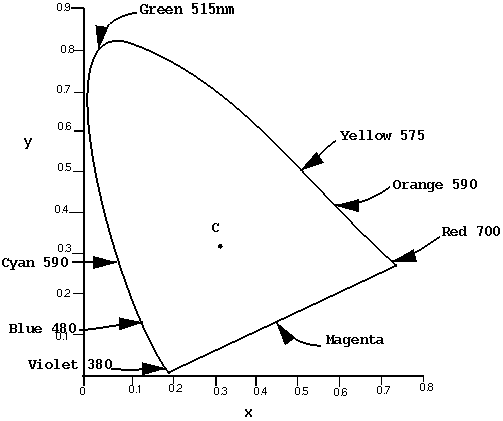
- 1 marks:
On this monitor, what is the dominant wavelength of a colour
with RGB=(1 0 1)?
- 3 marks:
Which pixels are set when drawing a line from (7,6) to (2,3)
using the midpoint algorithm?
- 3 marks:
Build the edge table for the following polygon:

Consider the following three illumination techniques:
| 1: | Phong local illumination |
| 2: | Non-distribution Ray tracing |
| 3: | Radiosity |
and the following five lighting effects:
| A: | view-independent illumination |
| B: | specular highlights |
| C: | soft shadows |
| D: | colour bleeding |
| E: | refraction |
Place check-marks in the following table if a technique can produce the corresponding effect.
| Technique | A | B | C | D | E |
|---|---|---|---|---|---|
| Phong local illumination | |||||
| Non-distribution Ray tracing | |||||
| Radiosity |
Using the following openGL calls:
glScalef (float x, float y, float z)
glTranslatef (float x, float y, float z)
glRotatef (float angle, float x, float y, float z)
glPushMatrix ()
glPopMatrix ()
and the function drawSquare(), which draws a square
with side length 1, centred at the origin:
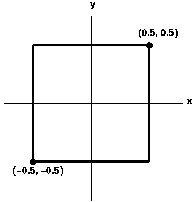
- 3 marks:
write the following function:
drawBox(float x, float y, float angle, float xsize, float ysize);which draws axsize×ysizerectangle, with one corner at (x,y), and rotated byangledegrees: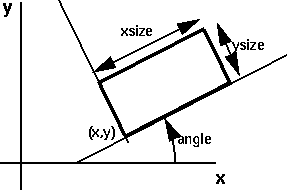
- 4 marks:
using the
drawBox()function you wrote, write code to draw the following object:

Consider the local-illumination model:
for the following polygon (represented as a line). Assume an orthographic projection.

- 2 marks:
On the diagram above,
sketch the vectors N, L, and V at points A, B and C on the polygon.
- 4 marks:
At points A, B and C, calculate the ambient, diffuse, and
specular contributions of the surface's colour.
Assume the following parameters:
-
Ii = 1.0
Ia = 0.5
ka = 0.2
kspec = 0.4
kdiff = 0.5
n = 4
- 2 marks:
What are T-vertices?
- 2 marks:
Why are T-vertices a problem for shading algorithms?