Using Geometric Transformations

The simplest method of modelling objects is to use primitives such as lines and polygons. In the following, M is the desired transformation matrix which transforms points (2D or 3D) to pixel coordinates. 
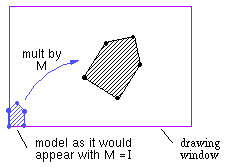
  for each vertex i
    new_vertex_list[i] = M * vertex_list[i]
  scanconvert( new_vertex_list )
Here is the equivalent in OpenGL:. 
  glBegin(GL_POLYGON);
  for each vertex i
    glVertex3fv( vertex_list[i] );
  glEnd();
There are several things to note: M can be setup as follows: 
  glMatrixMode( GL_MODELVIEW );
  glLoadIdentity();
  glTranslatef(2.0, 1.0, 0.0);
  glRotatef( -3.14/2.0, 0.0, 0.0, 1.0); 
  glScalef(2.0, 2.0, 2.0);
  ...
which produces the matrix M = trans(2,1,0) rot(z,-90) scale(2,2,2) ....
Another way of loading M is to use: 
  glMatrixMode( GL_MODELVIEW );
  glLoadMatrixf( M );

 

Transformation Hierarchies

Consider building the following model of a hand with one finger::
This can be constructed using a transformation hierarchy. In the following scene graph, circles represent transformations and squares represent geometry. The pseudocode on the left can be used to draw the scene.
 
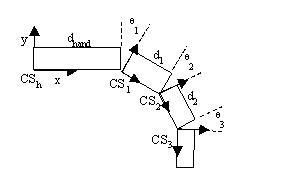
f1: trans(d_hand,0,0) rot(z,th1) 
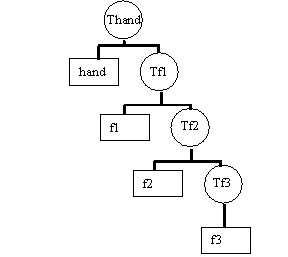
f2: trans(d1,0,0) rot(z,th2) 
f3: trans(d2,0,0) rot(z,th3) 

M=M*Thand 
draw hand 
M=M*Tf1 
draw f1 
M=M*Tf2 
draw f2 
M=M*Tf3 
draw f3

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
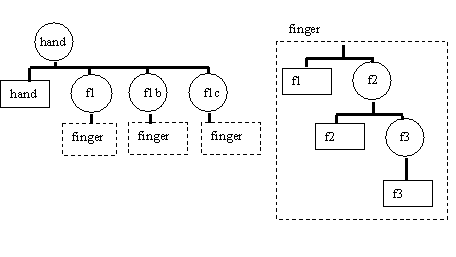
Now consider draw a hand with three identical fingers. We can create a more complex scene graph which uses multiple instances of a finger scene graph, as shown below. Because each of the fingers is defined relative to the hand coordinate system, a way is needed to restore the hand coordinate system before beginning to draw each finger. This is done through the pushMatrix() and popMatrix() function calls.
 
M=M*Thand 
draw hand 
pushMatrix() 
M=M*Tf1a 
draw_finger() 
popMatrix() 
pushMatrix() 
M=M*Tf1b 
draw_finger() 
popMatrix() 
pushMatrix() 
M=M*Tf1c 
draw_finger() 
popMatrix() 

draw_finger() { 
  draw f1 
  M=M*Tf2 
  draw f2 
  M=M*Tf3 
  draw f3 
} 
 

 

 Many graphics systems maintain a stack for the current transformation matrix: