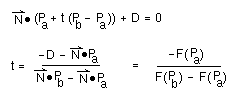[Hearn & Baker: p. 307-309. Foley & van Dam: p. 271-278]
Plane Equations
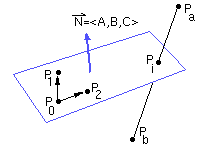
Implicit plane equation
Ax + By + Cz + D = F(x,y,z)
F(x,y,z)=0 for points on the plane
This can be rewritten as:
F(P) = N.P + D
Parametric plane equation
Plane(s,t) = P0 + s(P1-P0) + t(P2-P0), provided
P0, P1, and P2 are non-colinear.
Plane(s,t) = P0 + s V1 + t V2, where V1 and V2 are two
basis vectors.
Explicit plane equation
z = -(A/C)x - (B/C)y - D/C , valid if C is non-zero.
Line-plane Intersection
L(t) = Pa + t(Pb - Pa)
Substituting into the plane equation, and solving for t:
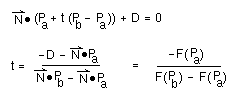
Clipping
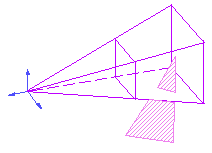
Both the Cohen-Sutherland line-clipping algorithm
and the Sutherland-Hodgman polygon-clipping algorithm can be extended
to 3D. We could choose to perform clipping in any one of
VCS, CCS, or NDCS. As we shall explain shortly, there is
a shortcoming to clipping in NDCS.
Clipping in VCS
Both the line-clipping and polygon-clipping algorithms made use of
in/out tests for half-spaces.
For the orthographic view volumes presented previously,
the view-volume plane equations can be written in a
consistent way, such that all the normals are pointing
into the view volume.
If F(P)>0, then P is inside the view volume.
left: x - left = 0
right: -x + right = 0
bottom: y - bottom = 0
top: -y + top = 0
front: -z - near = 0
back: z + far = 0
The same can also be done for the
perspective view volume:
left: x + left*z/near = 0
right: -x - right*z/near = 0
top: -y - top*z/near = 0
bottom: y + bottom*z/near = 0
front: -z - near = 0
back: z + far = 0
The Cohen-Sutherland clipping procedure works exactly the
same in 3D as it does in 2D. Vertex outcodes
are generated and tested for a trivial accept or reject.
If there is no trivial accept or reject, the line is clipped
against one if the six view-volume planes, then tested again,
and so on.
The Sutherland-Hodgman polygon clipping algorithm also
works in a similar way. The polygon can be clipped against
the six view-volume planes in succession.
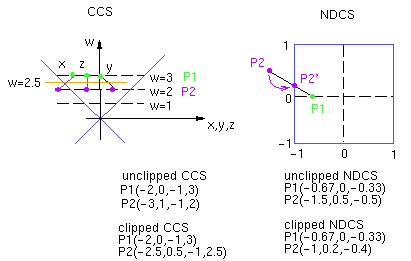
Clipping in NDCS
NDCS provides a potentially nice coordinate system for
clipping operations because the plane equations are
simply defined and always remain unchanged. Furthermore,
lines in VCS are lines in NDCS and therefore it would seem
that correct intersections can be calculated, despite the
fact that NDCS-space has a strange warp to it because
it is post-perspective division.
The potential problem of clipping in NDCS is that the sign
of the depth information is lost, as shown in the following example.
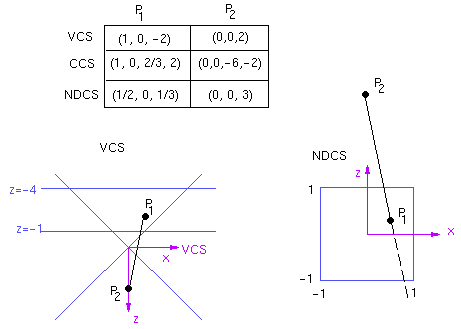
Clipping in CCS
We'll define the clipping region in CCS by first
looking at the clipping region in NDCS:
-1 <= x/w <= 1
This means that in CCS, we have:
-w <= x <= w
This can be visualized as follows:
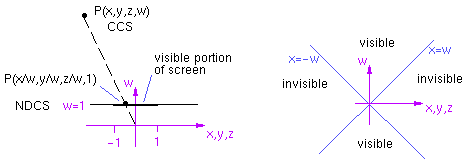
The clipping regions are analogous for y and z. The following example
illustrates clipping in CCS.