CSC418/2504F Fall 2001: Midterm Test:

Wednesday, October 31st, 2001, 1:00 PM

Family Name:_____________________________

First Name: _____________________________

Student ID: _____________________________

Instructions:

Attempt all questions.

There are five questions.

The total mark is 24.

You have 60 minutes to complete the test.

Aids allowed: Calculators

Textbooks and notes are NOT allowed.

1: /4

2: /5

3: /5

4: /5

5: /5

_________

Total: /24

1. Colour: [4 marks] A sheet of white paper is printed with four circles, coloured Yellow, Cyan, Magenta and Black. A Green light shines on the paper. Here is an RGB cube as a reminder:

a. [0.5 mark] What colour does the White background appear?

• Green. White reflects all wavelengths.

b. [0.5 mark] What colour does the Black circle appear?

• Black.

c. [0.5 mark] What colour does the Yellow circle appear?

• Green. Yellow reflects red and green.

d. [0.5 mark] What colour does the Cyan circle appear?

• Green. Cyan reflects blue and green.

e. [0.5 mark] What colour does the Magenta circle appear?

• Black. Magenta reflects blue and red, and there is neither red or blue in the light.

f. Now suppose a Yellow light shines on the paper.
[0.5 mark] What colour does the Yellow circle appear now?

• Yellow, of course.

g. [0.5 mark] What colour does the Cyan circle appear now?

• Green. Only the green component of the yellow (red+green) light is reflected.

h. [0.5 mark] What colour does the Magenta circle appear now?

• Red. Only the red component is reflected.

2. Projection: [5 marks] A unit cube lit by a point light at L(1,1,2) casts a shadow on the x-y plane:

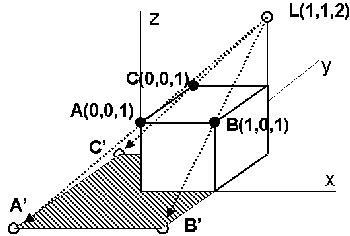
a. [2 marks] What are the coordinates of A', B' and C', the three corners of the shadow?

• A' = (-1,-1,0)
  B' = (1,-1,0)
  C' = (-1,1,0)

b. [3 marks] For an arbitrary point P(x,y,z), what are the coordinates of its shadow point P'(x,y,0) on the x-y plane?

• A line through L and P has the equation:
  Q = L + t*(P-L)
  Q = (1,1,2) + t*(x-1,y-1,z-2)
  The line crosses the xy plane when Q_z = 0, or
  0 = 2 + t*(z-2)
  t = 2/(2-z)
  So, the projected point P' is
  x' = 1 + 2*(x-1)/(2-z)
  y' = 1 + 2*(y-1)/(2-z)
  z' = 0
  

3. Visibility: [5 marks] Consider a set of polygons, represented in 2D cross-section as line segments. Arrows represent front-facing normals.

a. [3 marks] Draw the BSP tree obtained by inserting the polygons in alphabetical order. Left subtrees correspond to the front side, and right subtrees to the back. If any polygons are split, label the fragments on the diagram and the tree.

b. [2 marks] For the given camera eye point, list polygons in the order they are drawn by the BSP traversal algorithm.

• C₁ subtree, A, B subtree
• C₁, E, A, F₁, B, C₂ subtree
• C₁, E, A, F₁, B, C₂, D, F₂

4. Clipping: [5 marks]

a. [2 marks] Describe the trivial accept/reject test for Cohen-Sutherland clipping.

• This is in the notes and the text. Basically, for each vertex, compute 4 test bits:
  B = (y < y_bot)
  T = (y > y_top)
  L = (x < x_left)
  R = (x > x_right)
  Then, compute the bit-wise AND of all the TBRL signatures all the vertices of the polygon. If the result is non-zero, don't draw the polygon.
  Else, compute the bit-wise OR of all the signatures. If the result IS zero, draw the polygon without clipping.
  Else, clip.

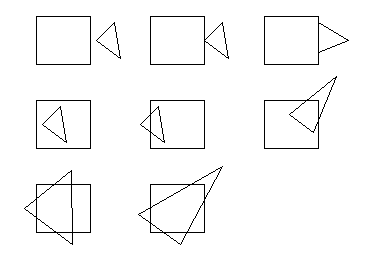
b. [3 marks] Suppose we clip a polygon with n sides against a rectangular window. The clipped polygon will have m sides, and often n ≠ m.

If n = 3, what values can m have? Give a sketch for each value of m.

• m can range from 0 to 7. Here is a sketch for each case:

5. Modeling: [5 marks] For this question, use the following openGL-like function calls:

trans(tx,ty)	scale(sx,sy)	rotz(ang)
glBegin()	push()	pop()

In this question, you will write code to draw a fractal “meander”.

Order 1	Order 2	Order 3

a. [1 mark] Write code to draw an order-1 meander.

•       order1 () {
          glBegin(GL_LINE_STRIP);
          vertex(0,0);
          vertex(0.3333,0);
          vertex(0.3333,0.3333);
          vertex(0.6666,0.3333);
          vertex(0.6666,0);
          vertex(1,0);
          glEnd();
        }
        
  

b. [4 marks] As you can see, an order-1 meander consists of 5 segments, each length 1/3. If we replace each segment with a whole meander scaled down by 1/3, we obtain a higher-order meander.

Write a function meander(int n) which draws an order-n meander. It is easiest to define the function recursively.

•       meander (int n) {
          if (n == 1) {
            order1();
          }
          else {
            push();
              scale(0.3333,1);
              meander(n-1);
            pop();
            trans(0.3333,0);
            rotz(90);
  
            push();
              scale(0.3333,1);
              meander(n-1);
            pop();
            trans(0.3333,0);
            rotz(-90);
  
            push();
              scale(0.3333,1);
              meander(n-1);
            pop();
            trans(0.3333,0);
            rotz(-90);
  
            push();
              scale(0.3333,1);
              meander(n-1);
            pop();
            trans(0.3333,0);
            rotz(90);
  
            push();
              scale(0.3333,1);
              meander(n-1);
            pop();
          }
        }