Geometric Transformations 2 -- Solutions

1. 
   
   
2. The point (x,y,0) maps to (x,y).
   The point (0,0,z) maps to -z*cos(30), -z*sin(30)).
   The point (x,y,z) maps to (x-z*cos(30),y-z*sin(30)). We can thus write:

   x' = x - z*cos(30)
   y' = y - z*sin(30)

   Writing this out in a 3x3 matrix gives:

    [ x' ]   [1 0 -cos(30) ] [ x ]
    [ y' ] = [0 1 -sin(30) ] [ y ]
    [ 0  ]   [0 0   0      ] [ z ]
   

   We could equally well have placed the transformation in a 4x4 matrix. The choice of what to do with z is arbitrary, as the question doesn't give any specifications about this.
   
   

3.  x' = (x+1)*w/2
    y' = (y+1)*h/2
   

4. 
   

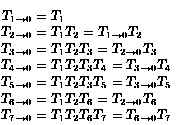
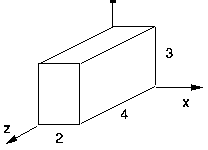
   Drawing the blocks:

       /* note: 'tm' denotes transformation matrix */
       /* assume tm for CS_0 is already setup before this code */
     glPushMatrix();      /* save a copy of original matrix */
   
     glMultMatrix(T_1);   /* setup for block 1 */
     draw_block();
   
     glMultMatrix(T_2);   /* setup for block 2 */
     draw_block();
   
     glPushMatrix();      /* save a copy */
     glMultMatrix(T_3);   /* setup for block 3 */
     draw_block();
   
     glPushMatrix();      /* save a copy */
     glMultMatrix(T_4};   /* setup for block 4 */
     draw_block();
   
     glPopMatrix();       /* restore T 3->0 */
     glMultMatrix(T_5);   /* setup for block 5 */
     draw_block();
   
     glPopMatrix();       /* restore T 2->0 */
     glMultMatrix(T_6);   /* setup for block 6 */
     draw_block();
   
     glMultMatrix(T_7);   /* setup for block 7 */
     draw_block();
   
     glPopMatrix();       /* restore original matrix */