The equation of the top plane of the view volume is:
y = -z tan(alpha) + top-near*tan(alpha)
The equation of the bottom plane of the view volume is:
y = -z tan(alpha) + bot-near*tan(alpha)
Any point on the top plane of the view volume should map to y' = 1. Similarly, any point on the bottom plane of the view volume should map to y' = -1.
y' can be written as a linear function of y and z:
y' = a*y + b*z +c
We'll set c=0 because from the diagram, the point y=0,z=0 should map to y'=0 (the center of the view volume). Note that this also fixes the angle alpha as being arctan( (top+bot)/2, near ).
To calculate the constants a and b, we'll substitute in the constraints for the mapping of the top-plane and bottom-plane:
1 = a*(-z tan(alpha) + top-near*tan(alpha)) + b*z
-1 = a*(-z tan(alpha) + bot-near*tan(alpha)) + b*z
This can be solved for a and b, yielding:
a = 2/(top-bot),
b = (a*top-1)/near
The final matrix thus looks like:
[ A 0 0 B ] [ 0 a b c ] [ 0 0 C D ] [ 0 0 0 1 ]where A, B, C, D are the same as in the orthographic case, and a,b,c are as defined above.
modelview transformation: 16x, 12+
projection transformation: 16x, 12+
division: 3/
viewport: 2x, 2+
Total for transforming 1 point: 34x, 26+, 3/
Total for transforming 3 points: 102x, 78+, 9/
Total flops per triangle: 102 + 78 + 5*9 = 225
10^6/225 = 4444 triangles per second
Note: For lighting calculations, surface normals also need
to be transformed, thus requiring some additional work.
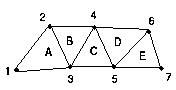
1 2 3 vertices 1,2,3 specify A 4 vertices 2,3,4 specify B 5 vertices 3,4,5 specify C ...