[Hill: 173-177. Foley & van Dam: p. 271-278]

Plane Equations


Implicit plane equation

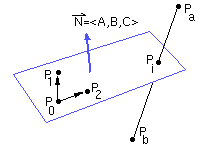
Ax + By + Cz + D = F(x,y,z)
F(x,y,z)=0 for points on the plane

This can be rewritten as:
F(P) = N.P + D

Parametric plane equation

Plane(s,t) = P0 + s(P1-P0) + t(P2-P0), provided P0, P1, and P2 are non-colinear.

Plane(s,t) = P0 + s V1 + t V2, where V1 and V2 are two basis vectors.

Explicit plane equation
z = -(A/C)x - (B/C)y - D/C , valid if C is non-zero.
Line-plane Intersection
L(t) = Pa + t(Pb - Pa)
Substituting into the plane equation, and solving for t:

Clipping

Hill: 386-390

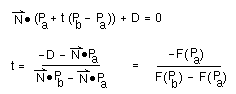
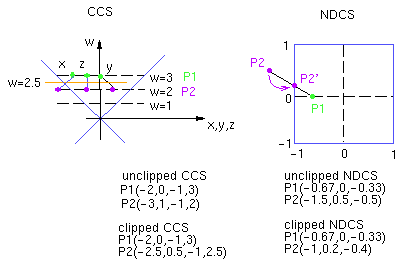
Both the Cohen-Sutherland line-clipping algorithm and the Sutherland-Hodgman polygon-clipping algorithm can be extended to 3D. We could choose to perform clipping in any one of VCS, CCS, or NDCS. As we shall explain shortly, there is a shortcoming to clipping in NDCS.

Clipping in VCS

Both the line-clipping and polygon-clipping algorithms made use of in/out tests for half-spaces. For the orthographic view volumes presented previously, the view-volume plane equations can be written in a consistent way, such that all the normals are pointing into the view volume. If F(P)>0, then P is inside the view volume. 
  left:    x - left = 0
  right:  -x + right = 0
  bottom:  y - bottom = 0
  top:    -y + top = 0
  front:  -z - near = 0
  back:    z + far = 0
The same can also be done for the perspective view volume: 
  left:    x + left*z/near = 0
  right:  -x - right*z/near = 0
  top:    -y - top*z/near = 0
  bottom:  y + bottom*z/near = 0
  front:  -z - near = 0
  back:    z + far = 0
The Cohen-Sutherland clipping procedure works exactly the same in 3D as it does in 2D. Vertex outcodes are generated and tested for a trivial accept or reject. If there is no trivial accept or reject, the line is clipped against one if the six view-volume planes, then tested again, and so on.

The Sutherland-Hodgman polygon clipping algorithm also works in a similar way. The polygon can be clipped against the six view-volume planes in succession.

Clipping in NDCS

NDCS provides a potentially nice coordinate system for clipping operations because the plane equations are simply defined and always remain unchanged. Furthermore, lines in VCS are lines in NDCS and therefore it would seem that correct intersections can be calculated, despite the fact that NDCS-space has a strange warp to it because it is post-perspective division.

The potential problem of clipping in NDCS is that the sign of the depth information is lost, as shown in the following example.


Clipping in CCS

We'll define the clipping region in CCS by first looking at the clipping region in NDCS:
-1 <= x/w <= 1
This means that in CCS, we have:
-w <= x <= w

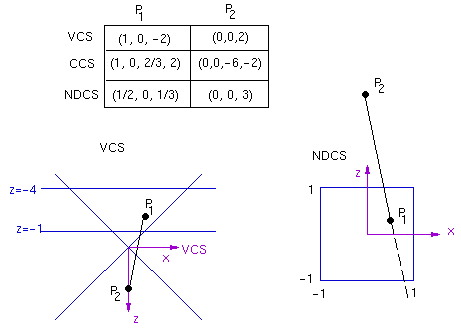
This can be visualized as follows:

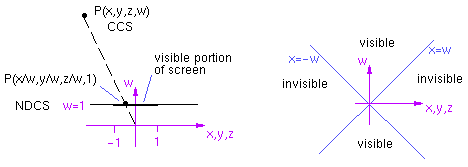
The clipping regions are analogous for y and z. The following example illustrates clipping in CCS.