[Hill: 244-247]

Transformations as a change of basis

There is another way of looking at transformations which can let us construct transformations between two coordinate systems directly, without having to express the transformations in terms of one or more rotation and translation operations.

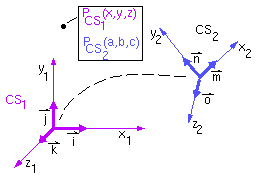
Suppose we have two coordinate systems, CS 1 and CS 2, having coincident origins, but having different orientations:


Let i,j,k and m,n,o be unit vectors as shown. These are called basis vectors.

The transformation between the two coordinate systems can be obtained as follows.


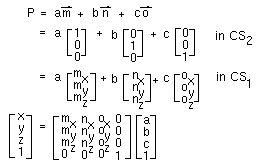
The elements of the top-left 3x3 portion of any geometric transformation are really the basis vectors of the local coordinate system expressed in the coordinates of the new coordinate system.