

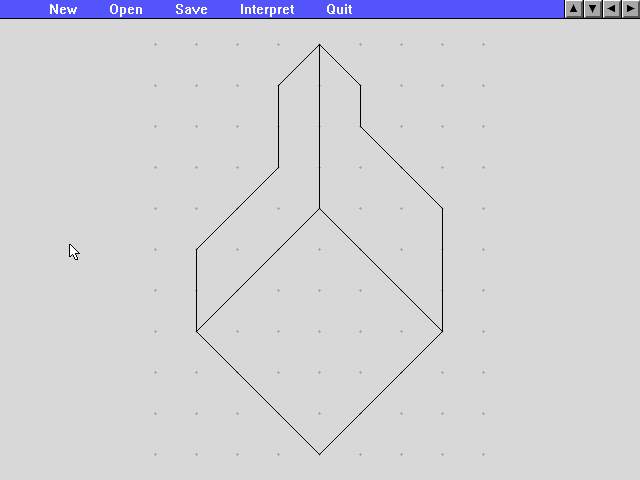
Step 2: the program attempts to label the edges of the drawing as convex (white), concave (black), or occluding (yellow). Arrows on yellow edges indicate which side of the edge corresponds to the occluding face. Edges whose type cannot be determined are shown in green.
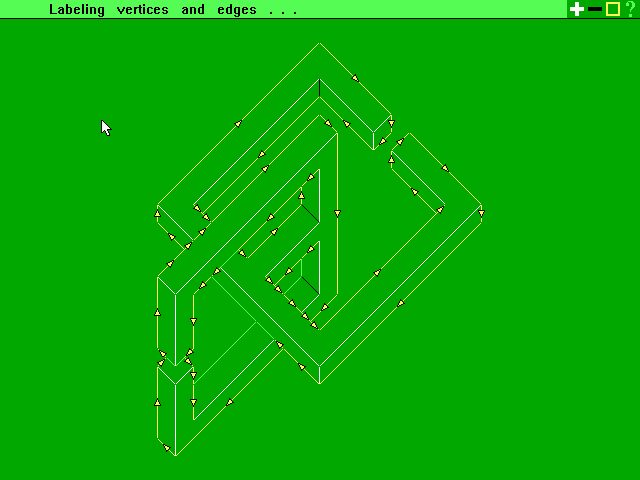
Step 3: the user manually enters the types of the green edges by using the arrow keys.
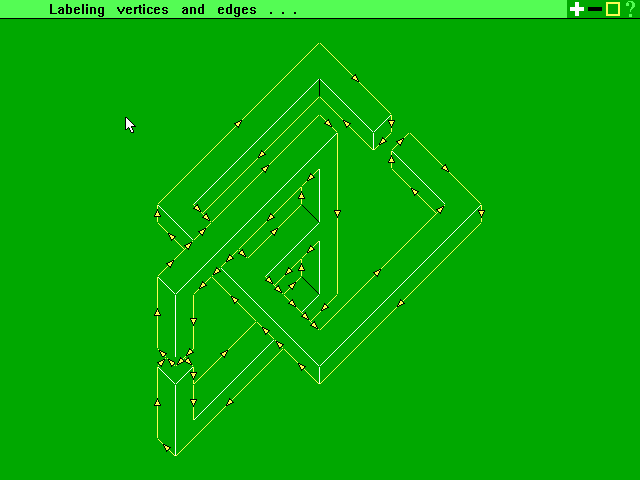
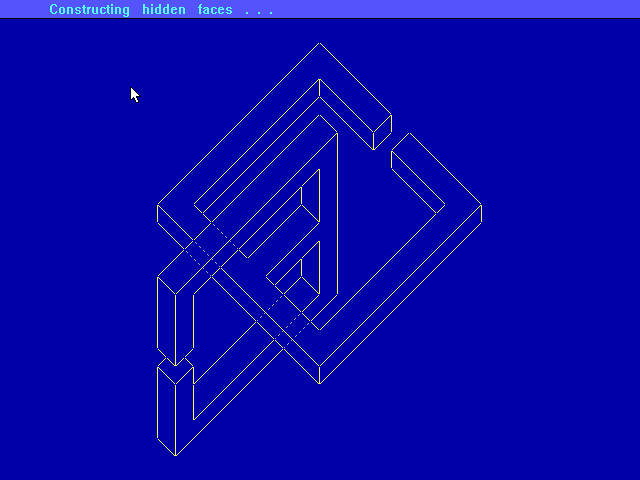
Step 4: after all the edges have been labelled, the program can attempt to construct the hidden edges of the object. Rays are cast out from all vertices having hidden edges, and intersections are computed until a complete object can be found (or until the program runs out of RAM !)
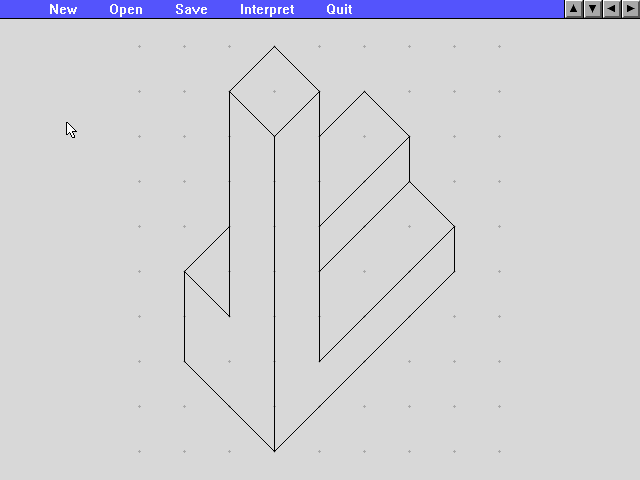
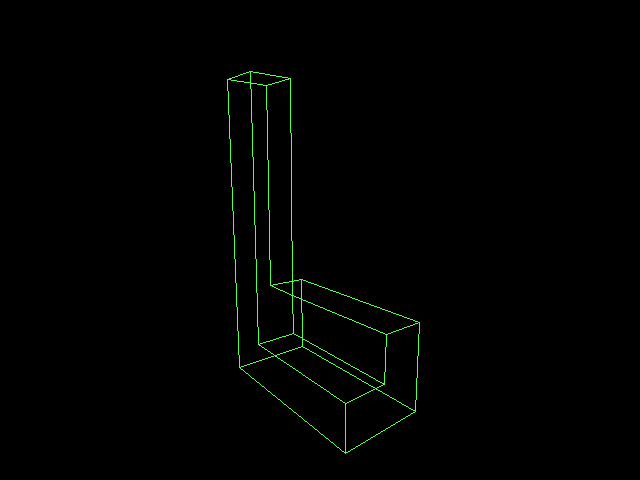
Step 5: if the program succeeds in constructing the object, a 3D wireframe is displayed that can be rotated with the mouse.


Here's a diagram showing all the edge intersections in 2D that the program was designed to handle. Red edges are convex, black edges are concave, and blue edges are occluding with the unoccluded face on the arrow's right side. Yellow regions are "empty space", i.e. not part of the polyhedron.
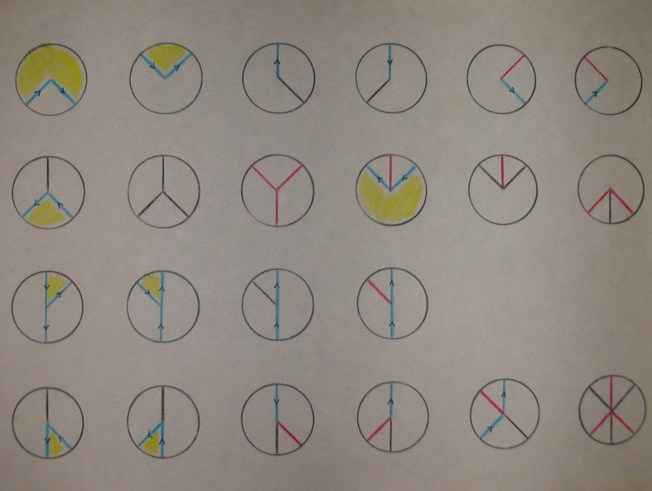
During the development of the 3D reconstruction algorithm, I built cardboard models of all the possible vertices, as an aid to visualization. Below, each cardboard model is shown from 2 different points of view.









