CSC418/2504F: Fall 2002 Assignment 2
Due: Wed. Nov. 6, 2002 in class.
- Transformations [4 marks] Consider the following
2-dimensional coordinate frames A and B and C.

- [2 mark] What are the coordinates of point P in frames A, B and C?
- [2 marks] What is the 3x3 homogeneous matrix MBC that, when
multiplied by a point in frame B, yields that point's coefficients in frame
C?
- Modeling [6 marks] A square pyramid is shown below.

- [4 mark] Give the transformations necessary to create a solid cube made
up of six pyramids. You can assume that the six initial pyramids all
start in the same location given above. Use simple notation like
rot(z,45) (counterclockwise rotation around z-axis by 45 degrees) and trans(2,3,4)
(here 2, 3 and 4 correspond to translation in the x, y and z directions) to indicate the transformations . Write the
set of transformation, in the right order, that each of the pyramids must be
multiplied by.
- [2 marks] What are the outward-facing unit normal
vectors for face EDC and vertex B?
- Ray Tracing (8 marks)
In ray tracing, primary rays are shot from the eye, through pixels, and tested
for intersection with objects. Write a program to intersect a primary ray with
an axis aligned ellipsoid, defined by the center C=<Cx,Cy,Cz> and radii
a,b,c, along the three axes XYZ. The equation of such an ellipsoid is (x-Cx)^2/a^2+(y-Cy)^2/b^2+(z-Cz)^2/c^2=1
The parametric form of a ray
starting at P, in direction V is (x,y,z) = P + t V , t>0.
Your program must read input from stdin in the example form....
0.5 1.6 2.7
2 4 7
8.3 9.1 -0.3
6.0 5.2 8.9
where the ray is defined by the its origin <0.5 1.6 2.7> and direction <2 4 7>
and the ellipsoid by center <8.3 9.1 -0.3> and radii along axes XYZ as 6.0,
5.2, 8.9 respectively.
The program should ouput the first intersection point to stdout if there is an
intersection and "no intersection" if there is no intersection between the ray
and the primitive.
Submit your code electronically, using one of the following commands:
submit -N a2q3 csc418h intersect.c
submit -N a2q3 csc2504h intersect.c
Submit a printed copy as well.
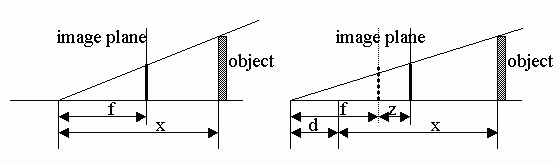
- Graphics pipeline [3 marks] A classic Hitchcock camera trick in the
film Vertigo was to dolly the camera away from a scene, yet preserve the film
size of objects by simultaneously zooming (changing the focal length) the
camera. This is shown below. x is the original distance between the
camera viewpoint and the object. f is the original focal length or
distance between the camera's viewpoint and its image plane. d is the
distance the camera is dollied back and z is the change in focal length
of the camera so that the object remains the same size on the image plane.
Write z as a function of d, f, and x.
- Hierarchies [9 marks] Write a program to draw and control the
four joint snake shown below. The snakes movement is limited to the
plane. The snake is anchored at one end, but can
freely rotate each of its four joints. When the user clicks on a point, the snake should move so that
its "head" is touching the point. If the point is out of reach, the
snake's head should point in the direction of the point.


- [1 mark] Draw the snake using four cuboids.
- [3 marks] The user should be able to click on
a point outside of the snake's reach. A red marker should be displayed
at this point. The snake should point towards the marker, as shown in
the first figure above. Simply adjust the first joint (theta 1) to
point the snake at the marker and keep every other joint at zero degrees. Each time the user clicks, the snake should move
so that it points at the new point. (Display a marker where the
last click was made.) NOTE: you do not need to animate the snake's
movement for parts B and C. It is acceptable to simply redraw the
snake in the new configuration when the user clicks at a new location.
This is equivalent to the snake moving instantaneously to the new
configuration. Only one snake should ever be displayed.
- [5 marks] Do the same as in part b, but deal with
any points within the snake's reach. Have the snake touch the marker
with its "nose". This is the case shown in the second figure. It
can be assumed that all targets will be above the line. Choose joint
angles so that the snake maintains a natural shape (2 marks).
Quantitatively, try to minimize the variation in angles theta 2 through
theta 4 (i.e. try to set them to have the same value.). Theta 1
can be freely varied. NOTE: as in part b, the transition to the new
configuration of the snake does not need to be animated. It is
sufficient to simply redraw the snake in the new pose.
- [3 marks] EXTRA CREDIT :
Animate it! Interpolate the joint angles to animate the
snake from its current position to its new position as defined in part b or
c. Achieve a transition time of two seconds.
Submit your code electronically, using one of the following
commands:
submit -N a2q5 csc418h snake.cpp ui.cpp
submit -N a2q5 csc2504h snake.cpp ui.cpp
Submit a
printed copy as well.
Sample code is available at:
http://www.dgp.toronto.edu/~neff/teaching/418/a2/code/





