




Next: 3.2.26 Partial Binary Functions
Up: 3.2 Constant Interval Arithmetic
Previous: 3.2.24 Charts
Consider the multiplication function, g(x,y) = xy,
An example evaluation follows:
For interval arguments that lie within one of the sections of 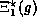 ,
two applications of
,
two applications of 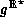 are used. For interval arguments which span two
sections of
are used. For interval arguments which span two
sections of 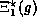 , four applications of g are used,
as was done in the above example evaluation.
Since g is continuous, we may reduce the number of applications of
, four applications of g are used,
as was done in the above example evaluation.
Since g is continuous, we may reduce the number of applications of 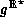 .
.
Consider evaluating g(x,y), for the situation depicted below.
The argument, (x,y), is covered by two sections of 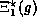 :
The sections share a common boundary, and points on the boundary are
not strict local maxima or minima of g.
This is true above, as both horizontal arrows point similarly, while
the common boundary is vertical.
With such a situation,
It follows that
:
The sections share a common boundary, and points on the boundary are
not strict local maxima or minima of g.
This is true above, as both horizontal arrows point similarly, while
the common boundary is vertical.
With such a situation,
It follows that 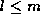 ,
, 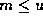 , so:
The bounds of
, so:
The bounds of 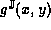 may therefore be computed with
two applications of g, rather than four.
With the common binary functions, this situation always occurs when an argument
spans two sections, unless the function is discontinuous at the common boundary.
If the function is discontinuous at the common boundary, then
the function is
may therefore be computed with
two applications of g, rather than four.
With the common binary functions, this situation always occurs when an argument
spans two sections, unless the function is discontinuous at the common boundary.
If the function is discontinuous at the common boundary, then
the function is 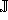 -bumpy.
Similar reasoning may be used when the argument spans four sections,
to reduce the number of applications of g from eight to four.
Concern for efficiency is focussed on evaluation of
-bumpy.
Similar reasoning may be used when the argument spans four sections,
to reduce the number of applications of g from eight to four.
Concern for efficiency is focussed on evaluation of
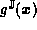 when
when 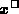 is small.
is small.





Next: 3.2.26 Partial Binary Functions
Up: 3.2 Constant Interval Arithmetic
Previous: 3.2.24 Charts
![]()
![]()
![]()
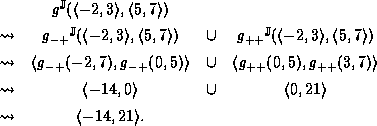

![]()
![]()
![]()
![]()