next up previous notation contents
Next: 3.2.27 Example with a Partial Up: 3.2 Constant Interval Arithmetic Previous: 3.2.25 Examples with a Binary

3.2.26 Partial Binary Functions

Partial functions are handled as before. Let g denote a partial binary function. The domain of g may be defined in terms of 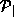tex2html_wrap_inline33463 :

math16574

The function 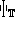tex2html_wrap_inline34937 ,

math16578

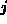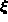again describes the relationship between tex2html_wrap_inline33497 and tex2html_wrap_inline35453 :

math16584

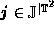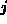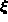where tex2html_wrap_inline35459 and tex2html_wrap_inline35461 . The relationship between tex2html_wrap_inline33497 and tex2html_wrap_inline35453 is that of containment, defined componentwise:

math16590

For the function 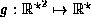tex2html_wrap_inline35191 , an evaluation of the model tex2html_wrap_inline34927 proceeds as follows:

math16596

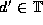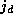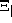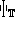The resulting domain description d', tex2html_wrap_inline34957 , is determined using tex2html_wrap_inline35477 , tex2html_wrap_inline35479 , tex2html_wrap_inline34961 , and tex2html_wrap_inline34937 :

math16607

The resulting value v' depends on d', as the value depended on the domain for partial functions.

The methods for handling discontinuous and 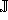tex2html_wrap_inline32653 -bumpy functions are similarly extended.

next up previous notation contents
Next: 3.2.27 Example with a Partial Up: 3.2 Constant Interval Arithmetic Previous: 3.2.25 Examples with a Binary
Jeff TupperMarch 1996