We now prove that the rules given in section ![]() ,
for constructing a
,
for constructing a ![]() chart, are correct.
chart, are correct.
The forbidden region is clearly correct since ![]() is a function;
we simply decree that
is a function;
we simply decree that ![]() as our use of the
as our use of the
![]() chart does not depend on how such points
are treated.
For (x,y) in the zero region,
chart does not depend on how such points
are treated.
For (x,y) in the zero region,
![]() and
and ![]() ;
so for any point in the zero region
;
so for any point in the zero region
![]() , which implies
, which implies ![]() .
.
For the remaining regions, consider the polynomial
![]()
![]()
![]()
![]()
Consider the point (x,y) which is ![]() away from
away from ![]() :
:
![]()
![]()
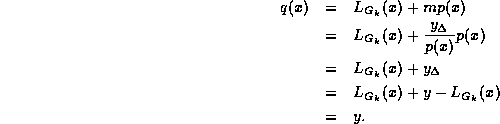
Earlier we proved q(x) interpolated ![]() for any m.
We have now shown q(x) interpolates
for any m.
We have now shown q(x) interpolates ![]() .
The leading coefficient of q(x) is m. The sign of m
relates to
.
The leading coefficient of q(x) is m. The sign of m
relates to ![]() : the sign of m is positive
if the region (x,y) resides in is labelled with
: the sign of m is positive
if the region (x,y) resides in is labelled with ![]() ;
the sign of m is negative if the region (x,y) resides
in is labelled with
;
the sign of m is negative if the region (x,y) resides
in is labelled with ![]() .
.
| Jeff Tupper | March 1996 |