Next: 3.2.4 Constant Functions
Up: 3.2 Constant Interval Arithmetic
Previous: 3.2.2 Interpolating Polynomials
Consider the following chart:
The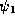 
chart is used to predict the sign of 
,
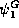for 
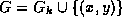, given 
.
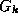The chart divides 
into six disjoint regions, as listed below.
- The forbidden region, indicated above by a dashed line.
The point (x,y) may not reside in the forbidden region,
since G is a function.
The remaining five regions are each labelled with a member of
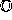. - The zero region, indicated above by a solid line, and labelled
with 0.
- Two up regions, each labelled with
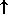. - Two down regions, each labelled with
.
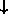If the point (x,y) resides in a region labelled with
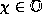, then 
.
The rules for constructing a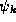 
chart are as follows:
-
The forbidden region, where
,
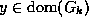is indicated by a dashed line. -
The zero region, where
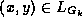, is labelled with 0.
The zero region, along with the forbidden region divide the remainder of
into a checkerboard of regions. -
The upper right region is an up region, labelled with .
-
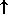The remaining regions are up and down regions, labelled with 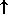and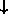
in checkerboard fashion, as shown above.
These rules work for any 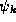chart, and are
defended in section 
.
There is a special case; when
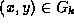the sign of 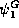is arbitrary.
This is forbidden with the above rules, since
.
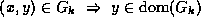These undercontrained cases are not important to us.
Next: 3.2.4 Constant Functions
Up: 3.2 Constant Interval Arithmetic
Previous: 3.2.2 Interpolating Polynomials
