




Next: 2.11.5 Simplicity
Up: 2.11 Interval Function Domains
Previous: 2.11.3 Domain Descriptions
A variation of 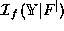 is the number system
is the number system 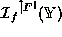 :
:
The number system
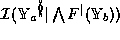 generalizes the number system
generalizes the number system
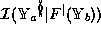 by allowing a set of constraints to describe an interval's domain.
Each interval
by allowing a set of constraints to describe an interval's domain.
Each interval
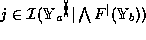 can be described by a value
can be described by a value 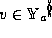 and a set of domain constraints
and a set of domain constraints 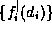 ,
with
,
with 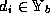 and
and 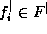 .
.
Parameter value 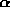 is in the domain of interval
is in the domain of interval
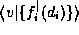 if
if
The definitions of interval inclusion and interval extension are
written as before,
but with the new semantics behind parameter inclusion.
The demotions 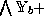 and
and 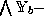 demote from
demote from 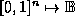 to
to
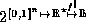 . As before,
. As before, 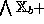 and
and 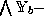 must preserve domain classifications.
must preserve domain classifications.
The implementation of models is simpler in
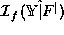 than in
than in 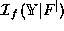 .
A description of a simple implementation of a model
.
A description of a simple implementation of a model
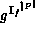 , of function
, of function 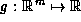 ,
follows.
,
follows.
-
If g is total,
an evaluation of
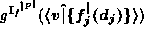 would return an interval with a domain described by
would return an interval with a domain described by
 .
. -
If g is partial,
an evaluation of
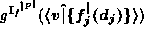 would return an interval with a domain described by
would return an interval with a domain described by
 ,
where
,
where 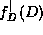 is a domain constraint introduced by
is a domain constraint introduced by
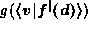 .
.





Next: 2.11.5 Simplicity
Up: 2.11 Interval Function Domains
Previous: 2.11.3 Domain Descriptions
![]() is the number system
is the number system ![]() :
:
![]()
![]() generalizes the number system
generalizes the number system
![]() by allowing a set of constraints to describe an interval's domain.
Each interval
by allowing a set of constraints to describe an interval's domain.
Each interval
![]() can be described by a value
can be described by a value ![]() and a set of domain constraints
and a set of domain constraints ![]() ,
with
,
with ![]() and
and ![]() .
.
![]() is in the domain of interval
is in the domain of interval
![]() if
if
![]()
![]() than in
than in ![]() .
A description of a simple implementation of a model
.
A description of a simple implementation of a model
![]() , of function
, of function ![]() ,
follows.
,
follows.