




Next: 2.12 Property Tracking
Up: 2.11 Interval Function Domains
Previous: 2.11.4 Conjunctions
A simple interval arithmetic which handles
partial functions gracefully is
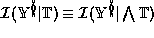 :
:
This is not an utter abuse of notation, as 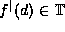 for any
for any 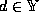 : every member
of
: every member
of 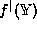 may be described as a member of
may be described as a member of 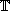 .
Furthermore, any non-trivial
.
Furthermore, any non-trivial 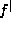 warrants the full descriptive power of
warrants the full descriptive power of 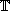 .
A trivial
.
A trivial 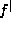 may be simulated by appropriately constructing
may be simulated by appropriately constructing
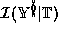 models.
models.
Consider the square root operator, denoted here as g.
It is a unary partial function, undefined for negative arguments.
Consider using 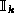 :
: 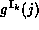 is
undefined if j contains only negative numbers. Consider the
following examples:
is
undefined if j contains only negative numbers. Consider the
following examples:
This illustrates one approach implementations may take when
confronted with partial functions.
Another approach is shown in the next section.
Another pair of examples follow:





Next: 2.12 Property Tracking
Up: 2.11 Interval Function Domains
Previous: 2.11.4 Conjunctions
![]() :
:
![]()
![]() :
: ![]() is
undefined if j contains only negative numbers. Consider the
following examples:
is
undefined if j contains only negative numbers. Consider the
following examples:
![]()
![]()
![]()
![]()