




Next: 3.2.13 Examples with Monotonic Functions
Up: 3.2 Constant Interval Arithmetic
Previous: 3.2.11 Monotonically Decreasing Functions
We have concentrated on upper bounds since lower bounds may be
easily constructed using the rules given for upper bounds.
This is achieved with the following identity:
which follows directly from the definition of extremal bounds.
Given that 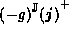 is an upper bound of
is an upper bound of 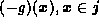 ,
it follows that
,
it follows that 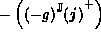 is a lower
bound of
is a lower
bound of  :
:
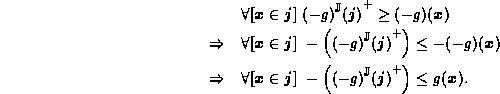
The proof is valid for all 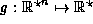 since it only relies on properties of
since it only relies on properties of  .
.
So both lower and upper bounds for 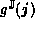 may be constructed
from the upper bounds of
may be constructed
from the upper bounds of 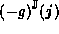 and
and 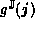 :
:
A similar process allows construction with lower bounds:
We do assume that the number system underlying the interval number system
has an exact negation operator which is total. Although the above construction
could be taken literally, it is mainly a device to simplify exposition.
In practice, upper and lower bounds are usually computed simultaneously
by a single procedure.





Next: 3.2.13 Examples with Monotonic Functions
Up: 3.2 Constant Interval Arithmetic
Previous: 3.2.11 Monotonically Decreasing Functions
![]()
![]()
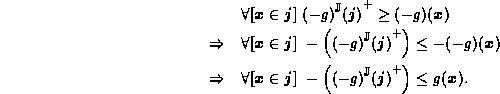
![]() since it only relies on properties of
since it only relies on properties of ![]() .
.
![]() may be constructed
from the upper bounds of
may be constructed
from the upper bounds of ![]() and
and ![]() :
:
![]()
![]()