Tutorial 
Geometric Transformations 2

1. Draw a cavalier projection of a block of size x=2, y=3, z=4. Use a 30-degree projection, i.e., the z-axis should make a 30-degree angle with the x-axis.
2. Give a projection matrix that produces the cavalier projection of question 1. Ensure that points lying the xy-plane are unaltered by the projection.
3. The gluViewport() function call is used to setup the transformation from normalized device coordinates to the display coordinate system, as shown below. Derive the necessary 2D transformation.


 
4. Consider the following scene with 7 blocks:


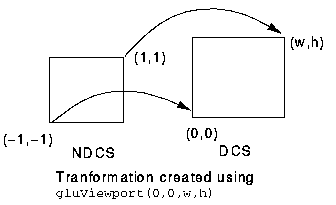
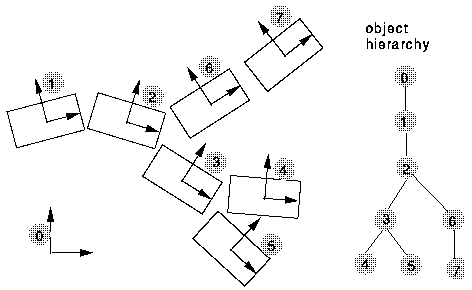
Let T_n define the transformation of block n with respect to its parent in the hierarchy, so that P_CSparent = T_n P_CSn.

For each block, determine the tranformation matrix required to transform its vertices to scene coordinates (CS0). Assuming that a block can be drawn using a function draw_block(), give the sequence of OpenGL function calls that might be used to draw the blocks, taking advantage of the matrix stack.

Suppose we wished to mount our synthetic camera on block 4, aligned with coordinate system of block 4. Find the transformation matrix that transforms points from the coordinate system of block 6 to the camera coordinate system.