Tutorial
Geometric Transformations 3

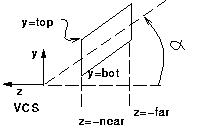
1. Derive the projection matrix for an oblique projection and view volume of the type shown below. It should map the given view volume into the same NDC coordinate system used in class and in OpenGL, namely one which is bounded by the cube -1<=x<=1, -1<=y<=1, -1<=z<=1. Assume that the view volume is not oblique when viewed from above.


 
2. Come up with an estimate of the number of multiplications, divisions, and additions necessary to do all the geometric transoformation work for a triangle. Suppose that floating point multiplications and additions take the same amount of time and that divisions take five times longer. How many triangles per second could be drawn if a 1 Mflop processor is used to do all the geometric transformations? Assume that the scan conversion of the polygon is not a bottleneck.
3. Suppose we are drawing a surface which is constructed using a mesh of connected triangles. Is there a way to take advantage of the connectivity to speed up the necessary transformations?