 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
25
|
 |
|
|
 |
|
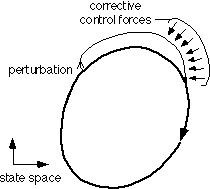
Figure 3.2 - An Active Limit Cycle
|
 |
|
|
|
 |
|
The problem of choosing appropriate control perturbations to drive the entire state of a system to a of a system to a
|
 |
|
desired value is a difficult one.
|
Assuming a solution does exist, the number of parameters to be
|
 |
|
determined is large for all but very simple systems (a few DOFs or less).
|
Non-linearities in  a a
|
 |
|
system mean that over the course of a full cycle even small perturbations of certain state variables
|
 |
|
can cause large changes in final state and/or result in almost no cycle at all.
|
For example, a small
|
 |
|
change in the roll angle of the ankle in a walk might cause the next foot to miss the ground
completely.

The essence of our control approach is to begin with a passively unstable system, discretize it into
|
 |
|
individual cycles and stabilize each cycle in turn.
|
Each cycle is stabilized by applying control
|
 |
|
perturbations which drive its final state to a suitable state from which to begin the next cycle.
|
The
|
 |
|
motivation for using a discrete version of the system is that the discrete dynamics are much
simpler to model than the continuous system and therefore, simpler to control, as we shall see
shortly.
|
 |

 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135

