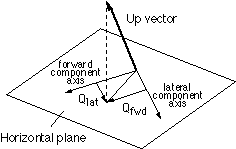
The RVs are two scalar components extracted from the given vector. The vector is sampled at the

end of the current step, normalized, and projected onto the horizontal plane.

The projection is

then decomposed into the two components as illustrated in Figure 3.13for the up-vector case.

The components provide an indication of the forward and lateral lean of the chosen vector. The

forward direction is defined as being orthogonal to the ground-plane projection of a line joining

the biped's hips.

Choice of Perturbation Parameters, [!]U

3. 6

The balance control formulation of Figure 3.6 uses two linear parametric perturbations (LPPs) to

control each step in the base PCG cycle.

Recall from Section 2.3 that each LPP consists of two

basic components, a fixed PCG perturbation, and a scalar multiplier. New values for each scalar

multiplier are automatically computed for each step to balance that step. The fixed part of the PCG

perturbations remain the same throughout a given walk. This section discusses the choice of fixed

PCG perturbations which must be supplied by the animator.

Throughout this section, the term

"perturbation" will be used to refer strictly to the fixed part of an LPP rather than an arbitrarily

scaled perturbation.