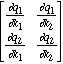50

In general, there is no guarantee that the discrete system Jacobian will be invertible for each step.

However, with well-chosen choices of RVs and LPPs, singularities generally occur only for

trajectories far enough from useful limit cycles to be of little interest.

Typical singularities for the

human model, occur when it is lying on its side and when the current stance leg does not contact

the ground at all during the current step.

The general form of the Jacobian for a 2D system is:

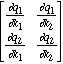
J=

(3.10)

Using finite differences, a minimum of N+1 samples are required to construct the linear model of

h(K) for a control system of dimension N: one for the nominal operating point and one for each

control dimension, each of which yields a column in the Jacobian.

In this case, each "sample"

consists of a simulation of one step with a different value of K.

samples may be required.

In practice, a greater number of

For the two dimensions of our bipedal control system, we use four sample simulations, two for

each dimension.

An additional simulation computes the final motion for the step after the final

PCG scalings have been chosen using the model.

choose to work with two simplified forms:

Rather than using the complete Jacobian, we

1. Assume independent control dimensions and observe only the primary RV.

This

corresponds to the assumption of a diagonal Jacobian (i.e. ðq_i / ðk_j= 0, i[!]j).

refer to this form as superposition(SP) sampling.

We will

2. Assume near-independent control dimensions but allow the operating point to move as

each final perturbation scaling is determined. This corresponds to a form of triangular