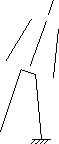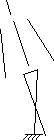|
Figure 3.15 - Typical effect of stance hip perturbations when dynamics are considered
 (a) right stance hip roll (a) right stance hip roll
 (b) right stance hip pitch (b) right stance hip pitch
|

The graphs illustrate that hip pitch varies nearly linearly with  Qfwd Qfwd for all three choices of RV. for all three choices of RV.
Similarly, hip roll is nearly linear with respect to Qlat. These relationships provide evidence which
supports our assumption that the discrete system can be modelled using a linear model. Despite the
fact that the perturbations themselves are mutually independent, their effect on the RVs is not
cleanly decoupled. Thus, they do not provide truly independent control over each RV dimension
|

 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135